시간 복잡도란(Time Complexity)?
알고리즘의 속도. 문제를 해결하는데 걸리는 시간과 입력의 함수관계.
입력이 많을수록 처리할게 많아지니까 시간이 더 걸린다.
알고리즘을 어떤 방식을 사용하냐에 따라 시간이 덜 걸릴수도, 더 걸릴수도 있다
이런식으로 입력과 해결의 관계를 나타낸 것이 시간복잡도이며, 당연히 시간 복잡도가 낮은 알고리즘이 효율성이 높다.
알고리즘의 속도의 표현방식이 왜 필요할까?
A가 B보다 빠르다. 사실 이 말로도 충분히 이해는 간다.
하지만 빠르다는 것 외에 추가적인 기준이 필요하다.
A가 B보다 결과가 빨리 나왔는데, 알고보니 A를 실행한 컴퓨터가 성능이 더 좋은 컴퓨터였다면??
스피드 경기를 진행할때도 같은 환경에서 같은 조건하에 타이머를 가지고 등수를 가리듯이 알고리즘에 대한 기준도 필요한것이다.
예를들어 같은 컴퓨터로 한 결과인지, 같은 에디터 또는 IDE를 사용했는지, 시작 시간이 같았는지 등등
기준이 있어야 정확히 무엇이 빠른지 느린지 구분할 수 있는것이다.
그럼 알고리즘의 속도를 평가하는 기준을 무엇으로 잡았을까?
바로 결과까지 수행되는 "절차의 수"를 기준으로 잡는다.
5번만에 결과가 나오는지, 10번만에 결과가 나오는지 등 단계의 수로 결정한다.
시간 복잡도 표기법 종류
Big-O (빅 오)표기법 : 알고리즘의 최악의 실행 시간을 표기.
Big- Ω(빅 오메가) 표기법: 알고리즘 최상의 실행 시간을 표기.
Big- Ω(빅 오메가) 표기법: 알고리즘 평균 실행 시간을 표기.
이 중 빅 오 표기법을 가장 많이 사용하고 있기에 빅오표기법에 대해 자세히 알아보자.
Big-O 표기법
표기 방법: O(n)
뜻: 가장 오래 결리는 경우만을 생각한다.
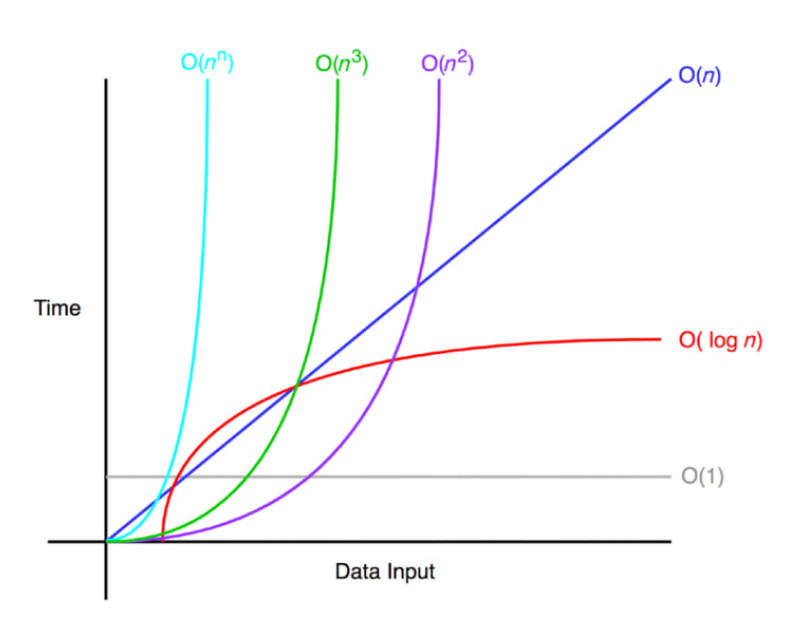
입력 크기 표현: O(1), O(), O(), O(), O(), O(), O()
ex) O(n) : 입력 n개에 대해 n번 처리
| 시간 복잡도 크기 순서 O(1) < O() < O() < O() < O(n) < O(2n) < O() |
입력 크기 예시
O(1) : print(10)
O(log n) : 이진탐색
O(n) : 반복문.
입력되는 n에 따라 결정되는 함수로, n의 크기에 따라 시간 복잡도가 늘어난다.
(입력이 클수록 시간이 많이걸리는건 당연한 이치)
O(): 중첩 반복문
타입과 메소드에 따른 시간복잡도
배열, 딕셔너리 등 타입에 따라, 메서드에따라 시간복잡도가 다르다.
코드 줄이 짧다고 무조건 효율적인 코드가 아니고 코드가 좀 더 길더라도 더 효율적일 수 있다.
따라서 알고리즘의 효율성을 높이고 싶으면 시간복잡도를 참고해서 만드는것이 좋다.
① List
리스트의 경우, 무작위로 찾는 것보다는 인덱스를 활용하거나 정렬하는것을 추천한다.
파이썬에 in을 활용해서 일치하는 요소를 찾는 문법이 있는데 이는 시간복잡도로 봤을때 효율적이지 않다.

② Dictionary
딕셔너리는 키:값 으로 묶여있기 때문에 값을 찾을때 리스트에 비해 시간복잡도가 낮다.

문제 요구사항에 따른 알고리즘 설계
*제한시간이 1초일 경우?
N의 범위가 500 : O(N3)
N의 범위가 2,000 : O(N2)
N의 범위가 100,000 : O(NlogN)
N의 범위가 10,000,000 : O(N)
파이썬 실행시간 측정하기
import time
start_time = time.time() # 측정 시작
#소스코드 입력
end_time = time.time() # 측정 종료
print("수행 시간: ", end_time-start_time)